本文摘取自我的另一项工作，主要是谈一谈我对补码的理解。
主流的教材，往往先介绍原码，然后是反码，最后是补码。到头来，公式倒是记住了，可是至于其“所以然”，却不甚明了。我感到，当初课上老师的介绍方式，当然是正确的，可是却引发了我不少的误解。
于是有此文。权当做抛砖引玉。

补码（Two’s Complement）是数字在计算机中的一种表示方式。

或许你会问，数字在电脑中难道不是用二进制表示的吗？你说的没错。让我们在讲解补码之前，先来了解一下二进制吧。

进制，或者说进位计数制是人类最常用的计数方法。在我们的日常生活中，我们使用的进制是十进制（Decimal）。所谓十进制，用一句话来说就是“逢十进一”。

例如，从0开始数数：0，1，2，3，4，5，6，7，8，9——当你数到9的时候，下一个就是十了。这个时候，由于我们没有一个单独的符号表示十，所以我们向十位进一，并将个位清零。这样，十就表示成了10。所谓“逢十进一”，就是当我们即将数到十的时候，向上进一位。

这对于二进制也是一样的。二进制用一句话来说就是“逢二进一”。二进制中只有两种符号：0和1。

让我们用二进制来数数吧：0，1——请注意，在这个时候，下一个数字就是二了，我们需要“逢2进一”。让我们仿照上面的做法，向上进位，并且把个位清零。这样，二在二进制下就表示为10。

同理，用二进制接着往下数，三是11，四是100，五是101，六是110，七是111，八是1000……请尝试从中找到规律，理解进制是如何运作的。

如果你无法理解以上内容的话，也没有关系，我们有一个简单的方法将二进制转换为十进制。首先，让我们再来审视一下我们最熟悉的十进制是如何运作的吧。

对于一个任意的十进制数字，它的值就等于每一位上的数字分别乘以每一位上的权重，最后相加。这个权值是多少呢？对于个位，权值是一；对于十位，权值是十；对于百位，权值是一百；对于千位，权值是一千……对于从右往左数的第n位，权值是。

例如，对于十进制数12345，它的值就是：（下面的公式中的数字都是十进制数字）

也就是：（下面的公式中的数字都是十进制数字）

请观察这些权值。它们都由两个部分组成：指数从低位向高位从0开始递增，而底数保持不变，为十。这个规律对二进制也是成立的，惟一的区别是：在二进制中，权值的底数是二。

例如，对于二进制数1010，它的值就等于：（下面的公式中的数字都是十进制数字）

以上就是将二进制数字转换为十进制数字的方法。

然而，在计算机中，数字并不总是这样表示的。很多时候，为了满足一些特殊的需要，我们需要对上面的表示法动一些手脚。比如，上面的方法用来表示正数是很好的。可是如果你要表示负数怎么办呢？

在计算机中，我们表示可正可负的整数——我们称之为“带符号的整型数”——的方法就是补码。接下来，我们将会一点点讨论补码的原理。

首先，计算机中存储的数范围往往是有限的。在存储数字的时候，我们需要为这个数字分配一块空间。如果分配得太大，就会造成浪费，因为计算机中的存储空间是比较昂贵的。因此，我们就需要估计这个数字的大概范围，并给它分配一个大小合适的空间。在现代的计算机系统中，一般来说，一个整数占用的空间是32位或者64位。如果我们想要用一个64位的空间存储一个非负整数，那么这个数的存储范围就是到。绝大多数时候，这都够用了。

为了简单起见，我们先假设这个数最多只有4位。那么它的范围是多少呢？用二进制来写，就是0到1111。转换成十进制，就是0到15。

这个时候，问题就产生了。如果你给二进制的1111加1，会发生什么呢？我们知道，二进制的1111加1应该等于10000，也就是十进制的16。然而别忘了，这个数字的存储空间最多只有4位，而10000有5位数，比限制多了一位。这个时候计算机会怎么处理呢？

答案非常简单。计算机会把最高位多出来的数字直接扔掉。这样，10000就变成了0000，也就是0。在计算机的视角下，1111加1就等于0。

如果我们把15乘以8，在二进制下就是1111乘以1000，又会怎么样呢？同理，虽然正确答案应该是1111000（十进制下的120），但是计算机会直接把超出四位的部分一股脑地丢掉，最后剩下的就只有1000了，也就是十进制的8。因此，在计算机眼里，如果一个整数的存储空间只有4位，那么15乘以8就等于8。

这种现象，我们称之为溢出（Overflow）。所谓溢出，就是指算出的结果超出了数字所能表示的范围。对于这种状况，计算机的解决办法就是把超出去的部分直接扔掉。下面我将用一个表盘形象地表示这种关系。

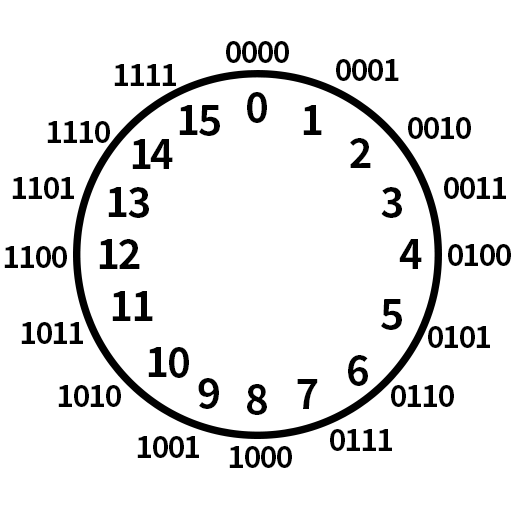
在这个表盘上，顺时针方向表示加，逆时针方向表示减。我们可以看到，从15顺时针走一个数字，也就是15加1，最终的结果等于0。同样地，从0逆时针走一个数字，也就是，结果等于15，写成二进制就是1111。

可是，我们都知道，应该等于，而不是15。计算机的早期设计者们正是注意到这一点，于是创造出了补码。既然计算机认为，可是实际上，那么我们能不能把15换成-1呢？这样的话，原本1111表示的是15，而现在表示的就是了。

实际上，现在的计算机就是这么做的。类似地，计算机认为，可是实际上，那么我们也可以把14替换成，用14的二进制形式1110来表示。到什么时候为止呢？到8被替换成了为止。这样的话，上面的表盘就变成了：

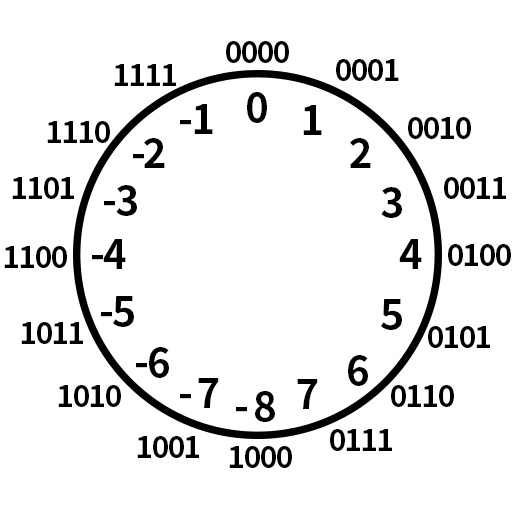
通过这种方式，我们就能够用二进制表示负数了。这就是补码。它的表示范围是到，也就是到。

为什么我们不把7也换成呢？因为我们希望补码的最高位可以体现出数的正负。如果最高位是1，那么就是负数；如果是0，那么就是非负数。这一条性质对于任何长度的补码都是成立的。而且，这样做可以让负数和非负数正好平分整个表盘。

那么，如果我用补码计算，岂不是变成了？如果我计算，最终的结果不就成了了吗？你说的没错。这种情况就叫做溢出。如果遇到了溢出，说明你应该换一种数据类型，让数字的范围变大一些。

类似地，如果是32位的补码，那么它的表示范围就是到。超出这个范围，就会发生溢出。

使用补码的好处是，在不发生溢出的情况下，我们只需要用平凡的二进制加法，就可以实现整数的加减运算。这减少了很多的麻烦。

我们有一种简单的方式求补码的绝对值。对于非负数，也就是最高位为0的数，绝对值就是它本身。对于负数，也就是最高位为1的数，对每一位取反（取反就是把0变成1，把1变成0），最后再加一。

例如，对于4位补码1001，求它的绝对值，首先把每一位取反，得到0110，然后再加1，变成0111。看看上面的表盘，你会发现0111表示的正是，而1001表示的是。

唯一的例外是1000，它表示，它的绝对值不能用上面的方法得出。如果你采用这个方法，需要对1000作特殊处理。